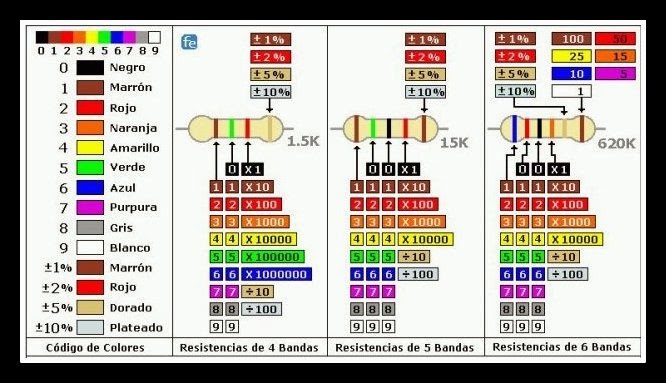
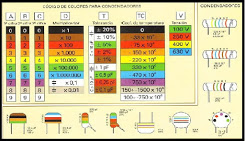
COMPONENTES ELECTRONICOS
Componente electrónico es un dispositivo que forma parte de un circuito electrónico.
Se encapsulan, generalmente en un material cerámico, metálico o plástico.
MANUALES

Manual de especificaciones y equivalencias de los transistores.
El manual contiene las descripciones, hoja de especificaciones de más de 100.000 transistores.
VER MANUAL....

Todos los MOSFET. Hoja de especificaciones. Equivalente. Principales características.
La selección de algunos parámetros de MOSFET. Equivalente de la búsqueda.VER MANUAL....

Dentro de los dispositivos SMD hay varios tipos de tamaños diferentes y encapsulados distintos.
Manual para su identificación.
Leer Más...